Étude des trajectoires et des vitesses de la boule et la quille après le choc
Mise en place de l'expérience
Mise en place de l'expérience
Pour étudier le choc, nous avons utilisé la même planche qu'auparavant, installée avec les mêmes paramètres afin de conserver les vitesses trouvées dans notre première expérience.
Nous avons ajouté à la toile cirée du sol une autre partie (découpée de la même toile cirée que nous avions utilisé au début).
Sur la toile cirée au sol nous avons marqué dans un début 3 positions pour la quille: A, B et C puis nous avons décidé d'en rajouter 3 autres: D, E et F. Notre but était de placer la quille à chacune de ces 6 positions et observer le choc pour chacune des positions et chacune des vitesses.
Pour cette deuxième expérience nous voulions obtenir les trajectoires et l'angle au sol c'est pourquoi le référentiel était différent de celui de la première expérience et nous avons filmé les vidéos de choc d'en haut en plaçant la caméra (HD cette fois-ci, puisque les caméras .avi ont été changées par les agents de laboratoire) au bout d'un support métallique fin et petit placé lui-même au bout d'un grand support métallique placé sur la table.
Nous avons modélisé la quille avec une petite quille de 42,95g du même jeu que la boule qu'on avait utilisée pour la vitesse et que l'on a réutilisée pour le choc.
Nous attendions comme résultats que les trajectoires de la quille et de la boule seraient les mêmes depuis chaque position A, B, C, D, E ou F indépendamment de la vitesse de la boule avant le choc. Nous attendions de même de voir que la quantité de mouvement et l'énergie cinétique étaient conservées après le choc.
 |
| Positions sur la toile cirée |
Les distances entre les points, choisies aléatoirement, sont:
CB = 2,5 cm
BA = 2,7 cm
AD = 2,0 cm
DE = 2,7 cm
EF = 2,0 cm
Leurs angles par rapport à la position A (choc frontal théorique) sont:
A = 0º
B = 4º
C= 7º
D = -3º
E = -6
F = -9º
Pour cette deuxième expérience nous voulions obtenir les trajectoires et l'angle au sol c'est pourquoi le référentiel était différent de celui de la première expérience et nous avons filmé les vidéos de choc d'en haut en plaçant la caméra (HD cette fois-ci, puisque les caméras .avi ont été changées par les agents de laboratoire) au bout d'un support métallique fin et petit placé lui-même au bout d'un grand support métallique placé sur la table.
.JPG) |
| Caméra placée pour filmer l'expérience d'en haut |
Nous avons modélisé la quille avec une petite quille de 42,95g du même jeu que la boule qu'on avait utilisée pour la vitesse et que l'on a réutilisée pour le choc.
Nous attendions comme résultats que les trajectoires de la quille et de la boule seraient les mêmes depuis chaque position A, B, C, D, E ou F indépendamment de la vitesse de la boule avant le choc. Nous attendions de même de voir que la quantité de mouvement et l'énergie cinétique étaient conservées après le choc.
Nous avons filmé 24 vidéos: 20A ; 20B ; 20C ; 20D ; 20E ; 20F; 40A ; 40B ; 40C ; 40D ; 40 E ; 40F ; 70A ; 70B ; 70C ; 70D ; 70E ; 70F ; 87A ; 87B ; 87C; 87D ; 87E et 87F.
Ensuite il a fallu transférer toutes les données des vidéos sur Avimeca et les étudier avec Regressi.
Analyse sur Avimeca
Voici quelques exemples de captures d'écran d'analyses de vidéos sur Avimeca.
Ceci est la capture d'écran de l'analyse d'une des vidéos (celle du choc 87 E). Il a fallu adapter la vidéo, le repère et l'échelle pour obtenir des résultats cohérents. Pour chacune des vidéos nous avons réalisé une analyse à 2 points: le point 1 est toujours la quille et le point 2 la boule.
.png)
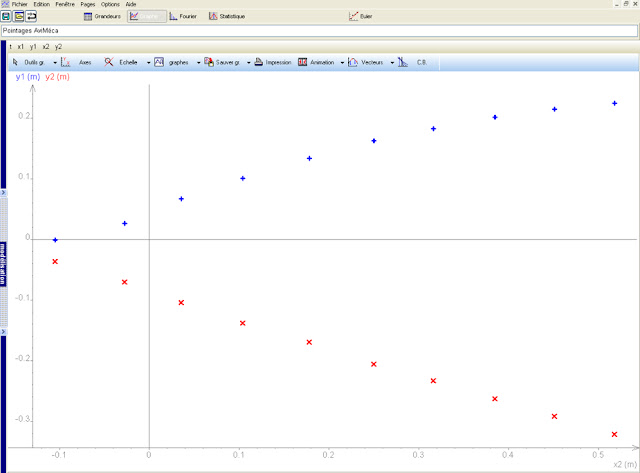
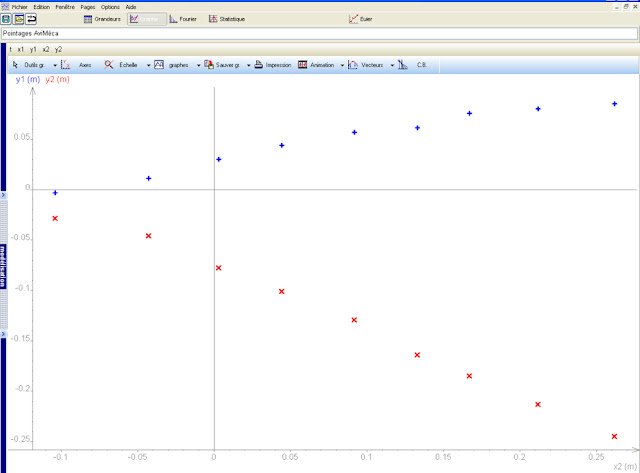
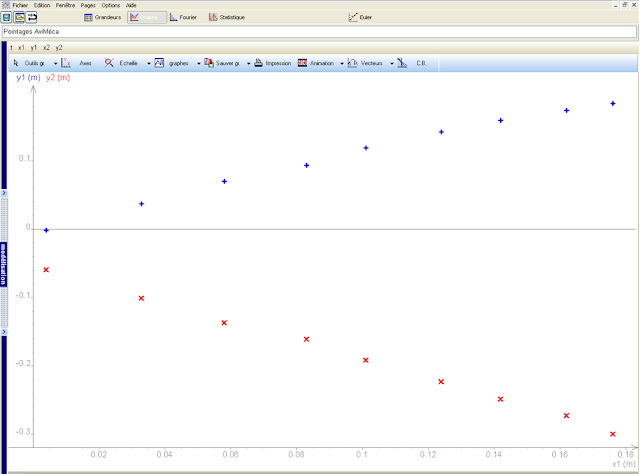
Voici les captures d'écran des trajectoires de la boule et de la quille obtenues sur Regressi, ainsi qu'un exemple de vidéo de choc pour chacune des positions A, B, C, D, E et F. La courbe bleue représente la trajectoire de la quille et la courbe rouge celle de la boule.
Position A
Exemple: vidéo des trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 20 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 20 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Trajectoires depuis la position 20 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Trajectoires depuis la position 20 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Trajectoires depuis la position 20 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Position C
Angle de déviation de la quille:
1ère capture d'écran: 26°;31°
2ème capture d'écran 22°;23°
Angle de déviation de la boule
1ère capture d'écran: -52°;-61°
2ème capture d'écran:-45°; -54°
Position D
Angle de déviation de la quille:
1ère capture d'écran: -18°;-16°
2ème capture d'écran -16°;-10°
Angle de déviation de la boule
1ère capture d'écran: 21°;24°
2ème capture d'écran: 22°; 28°
Position E
Angle de déviation de la quille:
1ère capture d'écran: -33°;-32°
2ème capture d'écran -36°;-35°
Angle de déviation de la boule
1ère capture d'écran: 28°;33°
2ème capture d'écran: 28°;32 °
Finalement, on voit que les angles de déviation de la boule et de la quille sont proches à chaque position (mais avec une marge d'erreur importante de plusieurs degrès). Ceci permet quand même de valider notre conjecture et affirmer que la déviation de la boule et de la quille est toujours la même pour sa position indépendamment de la vitesse avant le choc, même si dans la pratique on rencontre des incertitudes.
Voici le tableau récapitulatif des déviations de la quille et de la boule selon les différentes positions:
Après avoir réalisé ces expériences et obtenu des résultats à niveau expérimental, on se propose de vérifier les théorèmes de conservation de l'énergie cinétique et de la quantité de mouvement lors d'un choc élastique. Cliquez ci-dessous pour voir les calculs.
Vérification des théorèmes de conservation de l'énergie cinétique et de la quantité de mouvement
Ensuite il a fallu transférer toutes les données des vidéos sur Avimeca et les étudier avec Regressi.
Analyse sur Avimeca
Voici quelques exemples de captures d'écran d'analyses de vidéos sur Avimeca.
Ceci est la capture d'écran de l'analyse d'une des vidéos (celle du choc 87 E). Il a fallu adapter la vidéo, le repère et l'échelle pour obtenir des résultats cohérents. Pour chacune des vidéos nous avons réalisé une analyse à 2 points: le point 1 est toujours la quille et le point 2 la boule.
Voici d'autre part une capture d'écran à la fin de l'analyse sur Avimeca de la vidéo de choc 87 F. En effet on ne devrait pas l'appeler ainsi puisque la boule roulant depuis la position 87 n'arrive pas à frapper la quille sur la position F, il ne s'agit donc pas d'un choc à vrai dire.
.png)
Analyse des trajectoires sur Regressi
Position A
Exemple: vidéo des trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Position B
Exemple: vidéo des trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Position C
Exemple: vidéo des trajectoires depuis la position 20 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Position D
Exemple: vidéo des trajectoires depuis la position 87 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Position E
Exemple: vidéo des trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Position F
Voici les vidéos du choc 20F et 87F
20F
87F
On remarque que pour la position 20 F, le choc se produit tandis que pour les autres positions le choc ne se réalise pas sur F. Cette anomalie est due au fait que la vitesse de la boule à la position 20 est nettement inférieure à la vitesse de la boule dans autres positions.
Trajectoires depuis la position 20 sur la planche
Dans le but de démontrer la conjecture émise précédemment, on se propose de calculer mathématiquement l'angle de déviation de la quille et de la boule après le choc. Ce calcul se réalise par rapport à la position intiale de la quille (axe fixé sur Avimeca).
Voici, un exemple de trajectoire de la quille et de la boule après le choc. Rappelons que la courbe bleue représente la quille et la rouge la boule. Ainsi, on retrouve une configuration trigonométrique dans un triangle rectangle. (image ci-dessous)
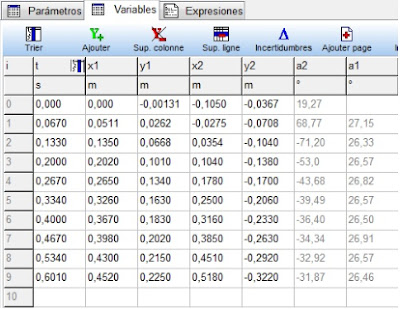
Grâce au tableur du logiciel Regressi, on effectue l'inverse de la tangente; atan(y1/x1) afin d'avoir une mesure (en dégrès) de l'angle, comme le montre la photo ci-dessous.
.tiff)
L'étude réalisée concerne les angles à toutes les positions. Voici, quelques exemples de résultats pour chaque position. D'une part, la colonne a1 représente la déviation de la quille, d'autre part la colonne a2 celle de la déviation de la boule.
Remarque: Il faut à nouveau dire que le pointage d'Avimeca est assez imprécis; on ne clique pas toujours exactement sur le centre de gravité des quilles ce qui fait que les trajectoires ne soient pas tout à fait exactes. Cette imprécision va se voir reflétée sur les tableaux de Regressi; on va voir ainsi des angles qui ne vont pas être toujours constants (pour une trajectoire rectiligne).
De même, la trajectoire de la boule n'est pas, au début, très rectiligne. C'est pourquoi, la valeur des angles de la boule va être faussée. On prendra donc les dernières valeurs de a2 pour la comparaison des tableaux.
Position A
Angle de déviation de la quille:
1ère capture d'écran: 2°;6°
2ème capture d'écran 9°;12°
Angle de déviation de la boule
1ère capture d'écran: -7°;-12°
2ème capture d'écran:-5; -13°
Position B
Angle de déviation de la quille:
1ère capture d'écran: 22°;23°
2ème capture d'écran 26°
Angle de déviation de la boule
1ère capture d'écran: -33°;-29°
2ème capture d'écran:-36°; -32°
20F
87F
Trajectoires depuis la position 20 sur la planche
Trajectoires depuis la position 40 sur la planche
Trajectoires depuis la position 70 sur la planche
Trajectoires depuis la position 87 sur la planche
Visuellement, après la réalisation de tous les vidéos, on peut conjecturer que les trajectoires de la quille et de la boule sont semblables depuis chaque position A, B, C, D ou E indépendamment de la vitesse de la boule avant le choc (voir CD). Le cas de la position F est spécial puisqu'avec les petites vitesses (positions 20 et 40 sur la planche) le choc a lieu et qu'avec les vitesses plus élevées (positions 70 et 87 sur la planche) il n'a pas lieu.
De même, après analyse sur Regressi, on constate que les trajectoires de la boule et de la quille sont semblables pour la plupart des positions.
Cependant, on remarque des courbes étranges, notamment pour 40A et 70A . On peut penser que ceci est dû au fait que lorsque la quille est à la position A, la boule la percute frontalement, en ligne droite.
Des anomalies au niveau des courbes peuvent aussi être dues à des erreurs de pointage sur Avimeca, comme c'est sûrement le cas pour les courbes 20B.
Analyse des angles de déviation sur Regressi
Voici, un exemple de trajectoire de la quille et de la boule après le choc. Rappelons que la courbe bleue représente la quille et la rouge la boule. Ainsi, on retrouve une configuration trigonométrique dans un triangle rectangle. (image ci-dessous)
Grâce au tableur du logiciel Regressi, on effectue l'inverse de la tangente; atan(y1/x1) afin d'avoir une mesure (en dégrès) de l'angle, comme le montre la photo ci-dessous.
L'étude réalisée concerne les angles à toutes les positions. Voici, quelques exemples de résultats pour chaque position. D'une part, la colonne a1 représente la déviation de la quille, d'autre part la colonne a2 celle de la déviation de la boule.
Remarque: Il faut à nouveau dire que le pointage d'Avimeca est assez imprécis; on ne clique pas toujours exactement sur le centre de gravité des quilles ce qui fait que les trajectoires ne soient pas tout à fait exactes. Cette imprécision va se voir reflétée sur les tableaux de Regressi; on va voir ainsi des angles qui ne vont pas être toujours constants (pour une trajectoire rectiligne).
De même, la trajectoire de la boule n'est pas, au début, très rectiligne. C'est pourquoi, la valeur des angles de la boule va être faussée. On prendra donc les dernières valeurs de a2 pour la comparaison des tableaux.
Position A
Angle de déviation de la quille:
1ère capture d'écran: 2°;6°
2ème capture d'écran 9°;12°
Angle de déviation de la boule
1ère capture d'écran: -7°;-12°
2ème capture d'écran:-5; -13°
Position B
Angle de déviation de la quille:
1ère capture d'écran: 22°;23°
2ème capture d'écran 26°
Angle de déviation de la boule
1ère capture d'écran: -33°;-29°
2ème capture d'écran:-36°; -32°
Position C
Angle de déviation de la quille:
1ère capture d'écran: 26°;31°
2ème capture d'écran 22°;23°
Angle de déviation de la boule
1ère capture d'écran: -52°;-61°
2ème capture d'écran:-45°; -54°
Position D
Angle de déviation de la quille:
1ère capture d'écran: -18°;-16°
2ème capture d'écran -16°;-10°
Angle de déviation de la boule
1ère capture d'écran: 21°;24°
2ème capture d'écran: 22°; 28°
Position E
Angle de déviation de la quille:
1ère capture d'écran: -33°;-32°
2ème capture d'écran -36°;-35°
Angle de déviation de la boule
1ère capture d'écran: 28°;33°
2ème capture d'écran: 28°;32 °
Finalement, on voit que les angles de déviation de la boule et de la quille sont proches à chaque position (mais avec une marge d'erreur importante de plusieurs degrès). Ceci permet quand même de valider notre conjecture et affirmer que la déviation de la boule et de la quille est toujours la même pour sa position indépendamment de la vitesse avant le choc, même si dans la pratique on rencontre des incertitudes.
Voici le tableau récapitulatif des déviations de la quille et de la boule selon les différentes positions:
Position
|
Quille
|
Boule
|
A
|
7°
|
-10°
|
B
|
24°
|
-33°
|
C
|
26°
|
-53°
|
D
|
-15°
|
23°
|
E
|
-34°
|
29°
|
Après avoir réalisé ces expériences et obtenu des résultats à niveau expérimental, on se propose de vérifier les théorèmes de conservation de l'énergie cinétique et de la quantité de mouvement lors d'un choc élastique. Cliquez ci-dessous pour voir les calculs.
Vérification des théorèmes de conservation de l'énergie cinétique et de la quantité de mouvement